Callan–Symanzik equation

Quantum field theory
(Feynman diagram)
History of...
Background Gauge theory Field theory Poincaré symmetry Quantum mechanics Spontaneous symmetry breaking
Symmetries Crossing Charge conjugation Parity Time reversal
Tools Anomaly Effective field theory Expectation value Faddeev–Popov ghosts Feynman diagram Lattice gauge theory LSZ reduction formula Partition function Propagator Quantization Renormalization Vacuum state Wick's theorem Wightman axioms
Equations Dirac equation Klein–Gordon equation Proca equations Wheeler–DeWitt equation
Standard Model Electroweak interaction Higgs mechanism Quantum chromodynamics Quantum electrodynamics Yang–Mills theory
Incomplete theories Quantum gravity String theory Supersymmetry Technicolor Theory of everything
Scientists Adler • Bethe • Bogoliubov • Callan • Candlin • Coleman • DeWitt • Dirac • Dyson • Fermi • Feynman • Fierz • Fröhlich • Gell-Mann • Goldstone • Gross • 't Hooft • Jackiw • Klein • Landau • Lee • Lehmann • Majorana • Nambu • Parisi • Polyakov • Salam • Schwinger • Skyrme • Stueckelberg • Symanzik • Tomonaga • Veltman • Weinberg • Weisskopf • Wilson • Witten • Yang • Yukawa • Hoodbhoy • Zimmermann • Zinn-Justin

In physics, the Callan–Symanzik equation is a differential equation describing the evolution of the n-point correlation functions under variation of the energy scale at which the theory is defined and involves the beta-function of the theory and the anomalous dimensions. This equation has the following structure

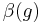$\left[M\frac{\partial }{\partial M}%2B\beta(g)\frac{\partial }{\partial g}%2Bn\gamma\right] G^{(n)}(x_1,x_2,\ldots,x_n;M,g)=0$

being $\beta(g)$ the beta function and $\gamma$ the scaling of the fields.

In quantum electrodynamics this equation takes the form

$\left[M\frac{\partial }{\partial M}%2B\beta(e)\frac{\partial }{\partial e}%2Bn\gamma_2 %2Bm\gamma_3\right]G^{(n,m)}(x_1,x_2,\ldots,x_n;M,e)=0$

being n and m the number of electrons and photons respectively.

It was discovered independently by Curtis Callan^[1] and Kurt Symanzik^[2]^[3] in 1970. Later it was used to understand asymptotic freedom.

This equation arises in the framework of renormalization group. It is possible to treat the equation using perturbation theory.

References

^ C. G. Callan, Jr., Broken Scale Invariance in Scalar Field Theory, Phys. Rev. D 2, 1541–1547 (1970). APS
^ K. Symanzik, Small Distance Behaviour in Field Theory and Power Counting, Commun. math. Phys. 18, 227 (1970). SpringerLink
^ K. Symanzik, Small-Distance-Behaviour Analysis and Wilson Expansions, Commun. math. Phys. 23, 49 (1971). SpringerLink

Literature

Jean Zinn-Justin, Quantum Field Theory and Critical Phenomena , Oxford University Press 2003, ISBN 0-19-850923-5
John Clements Collins, Renormalization, Cambridge University Press 1986, ISBN 0-521-31177-2

Callan–Symanzik equation

References

Literature

See also